«Yo os aconsejo dudar de todo, menos de que (...) dos y dos son cuatro.»

Voltaire (2005:169)

El presente artículo pretende conjugar las investigaciones y los resultados recientes de ciencia cognitiva con las prácticas en enseñanza de la matemática en la escuela primaria uruguaya.

Para la ciencia cognitiva actual, el cerebro humano posee desde el nacimiento información sobre cantidades que amplía y profundiza, en interacción con el ambiente y a través de los diferentes actores que intervienen en la vida del niño, para dar lugar al desarrollo de la aritmética. Posteriormente vendrá el álgebra, y junto con los aspectos geométricos serán los principales campos disciplinares que los maestros y los profesores intentaremos capturar en las diferentes evaluaciones del desempeño matemático.

Sin embargo, las pruebas estandarizadas muestran resultados de desempeño que no condicen con los esperados. Desde el sistema (Dirección General de Educación Inicial y Primaria) se proponen diferentes instrumentos y materiales para la mejora de los resultados, pero estos aún están por debajo de lo que se espera. Ello justifica que nos sigamos cuestionando las causas de estas dificultades y motiva la escritura de este artículo.

El trabajo intenta abordar este cuestionamiento, partiendo de la idea de que conocer respecto al funcionamiento de la mente humana en los primeros años de vida permite enriquecer la práctica docente en cuanto a la enseñanza de la matemática en la escuela primaria.

Desde sus orígenes, los números fueron incorporados naturalmente con el fin de resolver problemas de la vida cotidiana en el comercio, la arquitectura, la astronomía, etcétera.

Los números están presentes en nuestro entorno de forma continua, nos identificamos por el número de cédula de identidad, una talla, un número de teléfono, una dirección, una matrícula... Y hoy toda esta información numérica es procesada mediante inteligencia artificial, que aprende por su cuenta a partir de algoritmos.

Por esta razón, la pregunta sobre cómo se aprenden los números resulta determinante.

Su enseñanza le exige al docente una permanente revisión y actualización del contenido a fin de gestionar de forma eficiente la transposición didáctica. Al mismo tiempo necesita un docente con un conocimiento integral de la persona para quien es diseñada la enseñanza. En este caso, haremos foco en el aprendizaje inicial de matemática; por tanto, nos centraremos en las características del estudiante de primaria con relación al aprendizaje matemático de los números.

En educación se entiende la práctica docente como una praxis social que enfrenta situaciones, eventos y personas donde intervienen sentidos y significados, producto de las respectivas interrelaciones que se originan.

Ball, Thames y Phelps (2008) plantean que es necesario generar un entorno beneficioso para el aprendizaje y, al mismo tiempo, la necesidad de promover el intercambio entre los propios estudiantes con respecto al objeto matemático. Asimismo destacan la importancia que tiene el conocimiento sobre el objeto de enseñanza por parte de quien debe enseñar, y el valor de la profundización o la especialización en el conocimiento disciplinar de los maestros para desarrollar habilidades de enseñanza.

Los docentes que no conozcan en profundidad el contenido a enseñar podrían tener dificultades para ayudar a sus estudiantes. También se sabe que conocer bien el tema no siempre es razón suficiente para saber enseñarlo. Los referidos autores sostienen que es importante mapear este conocimiento matemático, porque al estudiar la relación entre lo que se debe enseñar y el logro de los estudiantes surge con claridad que el manejo del tema por parte de los docentes es un fuerte predictor de dicho logro.

Por otro lado, a través de distintos registros en videos 1 , Ball (2010) muestra que las interacciones grupales que se dan a partir de la reflexión entre los estudiantes con la guía del docente en torno al error, evidencian el propio conocimiento a través del encuentro con el resultado acertado. En este sentido, es importante la intervención docente con una pregunta que haga visible el error y con ello motive el intercambio y la corrección entre pares. Astolfi (1999) considera que el error es fuente de angustia y de estrés en la escuela. Hasta los alumnos que se consideran buenos tienen miedo a equivocarse. Sin embargo, enseñar a partir del error es orientar y guiar hacia la creatividad de los alumnos.

En esta idea coincide Boaler (2020), quien habla de la ciencia de los errores. El punto fundamental es trabajar con los niños en un ambiente donde se aprovechen los errores. Este proceso de aprendizaje y autoconocimiento contribuye a superar las propias barreras intelectuales.

Piaget (1978) sostenía que la adquisición del concepto de número aparecía alrededor de los cinco años, e iba precedido por un proceso de reconstrucción cognitiva continua que necesitaba de algunas habilidades de razonamiento lógico tales como la propiedad transitiva y la conservación de las cantidades para lograr la construcción de los conceptos matemáticos.

Diseñó ingeniosos procedimientos para estudiar la adquisición de los prerrequisitos del número (seriación, conservación, correspondencia), pero lo que nos dice la investigación empírica de las ciencias cognitivas al respecto es que, cuando a niños en etapas preverbales (algunos meses hasta el año aproximadamente) se les presentan situaciones análogas a las ideadas por Piaget, estas habilidades con los números progresan vertiginosamente.

Los avances de las investigaciones en neurociencia cognitiva han revelado que los bebés ya muestran un sentido numérico que está pronto para activarse desde el comienzo de la vida. A partir de la década de los ochenta, Izard et al. (2009) realizan experimentos con bebés y niños pequeños para evaluar sus facultades cognitivas. Sus investigaciones con relación a los rudimentos del conocimiento matemático muestran que los recién nacidos son capaces de detectar diferencias importantes en las cantidades (del triple) entre conjuntos de estímulos, concibiendo esto como una respuesta de tendencia matemática. Más adelante veremos que Starr, Libertus y Brannon (2013) plantean que los bebés un poco mayores pueden establecer relaciones con menor cantidad de objetos.

El psicólogo Steven Pinker adhiere a la corriente innatista.

«...la mente es un sistema de órganos de computación, diseñado por la selección natural para resolver aquellos tipos de problemas con los que se enfrentaron nuestros antepasados (...) La mente es lo que el cerebro hace (...) el cerebro procesa información y pensar es un modo de computar.» (Pinker, 2008:39-40)

Entonces, desde la concepción de la neurociencia cognitiva actual podemos decir que se viene al mundo con una serie de programas innatos con información desde los sentidos, que dan vida a las acciones y a los pensamientos que permitirán la interacción con la cultura.

En esta misma línea se encuentra Dehaene (2016)2 , quien aboga por la existencia de una base ontogenética de la matemática. Uno de los paradigmas experimentales utilizados por él apunta a demostrar que la noción de cantidad está presente en el bebé desde muy temprano. Se muestra que el bebé es capaz de cuantificar dirigiendo su mirada hacia donde hay más objetos. El experimento consiste en presentarle a un bebé (de cuatro meses de vida), imágenes que muestran diferente cantidad de objetos. El bebé deja de mirar la imagen después de cierto tiempo porque se aburre; pero si se le presenta una nueva imagen con más cantidad de objetos, nuevamente se atrae su atención, poniendo de manifiesto si su capacidad perceptiva es suficiente para detectar el cambio. Esto demuestra que los bebés tienen la capacidad intuitiva de reconocer cantidades diferentes, sin contar, en una etapa en la que la palabra todavía no es la herramienta de comunicación.

Estos y otros experimentos realizados en bebés demuestran que la comparación de cantidades forma parte de las competencias innatas que poseen distintas especies, incluida la humana.

Desde nuestra perspectiva, estos hallazgos refuerzan la idea de que la experiencia temprana con números es un elemento clave para el desarrollo cognitivo y, en particular, para el desarrollo de las competencias numéricas. Por lo tanto, la estimulación sobre objetos y números desde el comienzo de la vida parece ser un factor importante para el futuro del aprendizaje de las matemáticas. El aspecto fundamental entonces es preparar la transición de las capacidades no simbólicas, presentes desde muy temprano, a las capacidades simbólicas donde el número adquiere un significado más allá de la comparación de cantidades. Para reforzar este cambio a números simbólicos, familias, maestros y escuelas deberían desarrollar diferentes actividades (juegos con dados o con cartas, rompecabezas, dominós) que apunten a fortalecer el proceso de mapeo entre cantidades aproximadas de objetos y los símbolos exactos que representan la cantidad. Para contribuir y participar en este proceso, las intervenciones cognitivas se deben transformar en estrategias pedagógicas que los docentes puedan implementar en las aulas. Por ejemplo, actividades del Cuaderno para hacer Matemática en Primero (ANEP. CEIP. CACEEM, 2016:14-15) donde el niño, además de completar las grillas, debe conversar con sus pares sobre los resultados. El maestro estará atento a ese intercambio y observará in situ si se logró la transición de la que hablábamos antes.

Cuando se analizan en detalle los instrumentos empleados para evaluar el trabajo docente, se observa que los ítems que tenemos que valorar desde la inspección no contemplan estos conocimientos recientes que la ciencia cognitiva nos trae. Se evalúa la capacidad técnico-pedagógica, la conducción de los procesos de enseñanza y de aprendizaje, la orientación dada al curso, su planificación y su desarrollo, el clima de trabajo, la cooperación institucional e iniciativa, así como el trato dispensado a los alumnos; pero resulta difícil incorporar aquí su capacidad para adaptar las prácticas de aula al conocimiento reciente. La capacidad del docente de diseñar estrategias didácticas para la enseña de la matemática, que partan de los principios generales que intentamos esbozar más arriba y que son parte del acervo cultural actual que aporta la neurociencia cognitiva, debería integrar la evaluación que comencemos a hacer sobre el trabajo docente.

Al mismo tiempo, el docente valora la actuación de sus alumnos a través de diferentes evaluaciones externas: SEA (Sistema de Evaluación de Aprendizaje), LEO (Prueba de Lectura, Escritura y Oralidad), Aristas; así como de las propias pruebas diseñadas por el docente (internas), que informan sobre los resultados del aprendizaje. Sin embargo, la evaluación de logro a la que estas pruebas apuntan no captura (porque no han sido diseñadas para este fin) las habilidades cognitivas que, para el caso de la matemática, hoy sabemos que están en la base de los posteriores logros académicos, por ejemplo, la capacidad para distinguir cantidades de manera aproximada. Insistir en evaluar el cálculo mecánico a expensas del significado languidece la intuición matemática.

Los estudiantes poseen conceptos y destrezas relevantes para el aprendizaje de la matemática, que están presentes desde muy temprano en la vida. Este sentido numérico básico guía el aprendizaje de los símbolos y la aritmética. Dehaene (2016) sostiene que las personas nacen con circuitos cerebrales especializados en la identificación de números pequeños: un módulo numérico que permite la comprensión de cantidades y sus interrelaciones, lo que sirve de asiento al posterior desarrollo de las capacidades matemáticas más complejas. La reflexión docente debería ir en este sentido con la intención de construir «modelos mentales» (idem, p. 200) o repertorios personales de cálculo a partir de sus habilidades tempranas.

Starr, Libertus y Brannon (2013) respaldan la teoría de que el ser humano nace con un sentido numérico. Sus diferentes investigaciones realizadas con bebés sugieren que a los seis meses de edad son capaces de diferenciar entre cantidades con una razón de 2 (el doble) sin saber aún contar. La diferencia con las investigaciones de Izard et al. (2009) radica en la edad de los bebés con los cuales se llevaron a cabo los experimentos.

Concretamente, Starr, Libertus y Brannon (2013) muestran que aquellos bebés con mayor precisión en estas tareas de discriminación perceptiva a los seis meses, son los que presentan mejores desempeños en matemática al inicio de la escolarización, cuando adquieren los conocimientos de la matemática simbólica. La capacidad innata para la discriminación numérica es el sustento cognitivo para el aprendizaje escolar de las matemáticas formales.

Dehaene (2016) afirma que el consenso actual en cuanto al sentido numérico, es que se poseen dos sistemas de representación del número. Uno es el sistema de seguimiento de objetos, que permite seguir la trayectoria de objetos de no más de tres elementos. Este modelo mental fracasa cuando se encuentra frente a grandes cantidades de objetos. Otro es el sistema numérico aproximado, que puede representar pequeñas o grandes cantidades, y realizar comparaciones y operaciones entre conjuntos.

Estos cambios conceptuales en el reconocimiento del dominio del número fueron investigados por la psicóloga Susan Carey, quien sostiene que la noción de número posee un programa ontogenético, cuya explicación está dada por bootstrapping3 (arranque, inicio) que le permite conciliar capacidades básicas neurales que conforman representaciones mentales de los objetos con la cantidad de objetos en el espacio y en el tiempo.

Esta teoría nos anima a pensar que antes de ingresar a la escuela, el niño es capaz de subitizar, esto quiere decir que de un golpe de vista (conteo serial sin palabras) puede saber cuántos objetos hay en un conjunto de no más de cuatro elementos. Luego, al aprender el concepto de número, le sigue la estimación de cantidades, concepto mencionado muchas veces en el programa escolar vigente (ANEP. CEP, 2009), dando cuenta del pasaje de la numerosidad al conocimiento del número. En ANEP. CEIP. CACEEM (2016:69) se puede observar un ejemplo de actividad en la que se le solicita al estudiante que estime el resultado en una operación, generando un espacio de cálculo mental donde se ponen en juego las estrategias de cálculo personales y lo que aprendió en la escuela.

En el sistema numérico aproximado (ANS, del inglés Approximate Number System) se representa el número de una manera aproximada y comprimida, de tal manera que dos conjuntos pueden discriminarse si difieren en una proporción numérica determinada. Por ejemplo: si a un niño pequeño se le presentan imágenes con cierta cantidad de puntos y se le pide que indique dónde se encuentra el conjunto mayor, su respuesta será más rápida donde la razón entre ellos sea mayor (1 a 8, contra 8 a 9). Al parecer, los seres humanos nos guiamos por la razón (la proporción) entre cantidades para poder identificar las cantidades. Esto permite tener una medida sobre la capacidad de discriminación de cantidades que podemos esperar a cada edad, lo que se ha postulado como predictor de las competencias matemáticas formales posteriores.

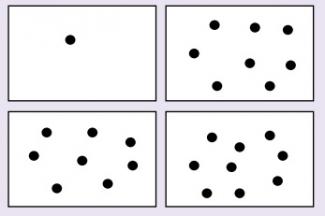
A través de la imagenología, Piazza (2010) prueba que este sistema tiene plausibilidad biológica. Se observa respuesta en el surco intraparietal, cuando se somete al sujeto a un experimento de comparación de conjuntos. Cuanto mayor es la diferencia entre conjuntos, más se activan las neuronas que responden a dicha diferencia en la imagen.

Las áreas visuales del cerebro reconocen un patrón, un dígito familiar e inmediatamente reconstruyen una representación continua y comprimida de una cantidad asociada a esa forma; es decir, cuando a un niño se le pide que piense en el número 5, tendrá una representación de ese símbolo, pero además podrá asociarlo en forma casi simultánea a una cantidad que estará representada por objetos o por sus dedos.

Lo anterior ocurre cuando son niños pequeños, pero cuando son un poco más grandes, ¿con qué frecuencia pueden distinguir con precisión la cantidad de personas que hay en una multitud? ¿Cuándo es más fácil precisar el número de individuos?, ¿cuando hay 10 o 55, 200 o 215? Entonces volvemos al problema de la estimación matemática (¿con qué estrategias cuenta y qué se le enseñó para resolver aquel problema?).

Otro dato interesante que nos revela la neurociencia es que siempre que el cerebro humano se enfrenta con un número, se apura a convertirlo en una cantidad analógica interna que preserva las relaciones entre cantidades y tiende a ubicarlo en una recta numérica mental. Esta solo codifica los números enteros positivos, ubica a la izquierda los números más pequeños y a la derecha los más grandes. El problema comienza cuando se debe encontrar significado y ubicación a otros números, como los racionales, los irracionales y los complejos. En las ejemplificaciones del programa escolar vigente (ANEP. CEP, 2009:386) se presenta una actividad relacionada con este tema.

Como vimos, el sentido numérico está presente en la vida desde muy temprano, está en nuestras manos usar dicho conocimiento como insumo para intervenciones didácticas y para incidir en la competencia matemática de nuestros estudiantes.

Las investigaciones realizadas en Uruguay con este mismo enfoque de neurociencia cognitiva destacan además que el contexto familiar, y específicamente el desarrollo de actividades matemáticas cotidianas durante la primera infancia, pueden significar un factor importante para el desempeño matemático. Se asume que existe una asociación entre la frecuencia con la que los niños realizan actividades numéricas en el hogar y el desempeño matemático en edades tempranas. Los resultados obtenidos por el equipo que dirige el profesor Alejandro Maiche en el Centro Interdisciplinario en Cognición para la Enseñanza y el Aprendizaje (CICEA - Udelar), sugieren que los niños que en sus hogares realizan mayor cantidad de actividades que implican la exposición a contenido numérico (juegos, libros, etc.), son los que a posteriori presentan desempeños más altos en matemática. Luego, la educación formal multiplica las facultades que el cerebro humano posee. Este despliegue de algoritmos cerebrales sucede de modo intuitivo, porque nadie explica las reglas para que el cerebro memorice, olvide, se equivoque o acierte.

El aporte de las ciencias cognitivas a la matemática completa y complementa el marco de referencia que sustenta la acción educativa porque, a partir de ellas, el docente puede interpretar el comportamiento de los alumnos en torno a esta disciplina para luego redirigir, orientar y organizar las intervenciones y decisiones pedagógicas.

La educación es un sistema complejo, al que no es posible acercarse desde una sola disciplina; por eso es necesario que para tener un mayor conocimiento de este sistema se conjuguen diferentes campos como neurociencia, psicología, pedagogía, filosofía, antropología, sociología, entre otros.

A ello debe agregarse que los procesos de enseñanza y de aprendizaje son modelados por varios elementos internos y externos a las personas. Por lo tanto, al momento de enseñar o de aprender son múltiples los factores que intervienen de forma más o menos significativa.

En este artículo se intentó exponer algunos de los elementos internos que debemos conocer para favorecer el aprendizaje, en este caso de la matemática en la escuela primaria.

A través de lo escrito queda claro que es preciso entender el comportamiento del niño, conociendo los rasgos del órgano que lo determina: el cerebro. A manera de resumen, sabemos que el niño reconoce numerosidades en etapas muy tempranas de la vida. Sabemos que esas cantidades se detectan fácilmente cuanto mayor es la razón entre los conjuntos comparados, y disminuye o aumenta según se vaya hacia la izquierda o la derecha de la línea mental. Todas estas afirmaciones y otras que exceden las posibilidades de este artículo tienen su correlato neural observado efectivamente en representaciones de imágenes cerebrales, y resultan importantes para nuestra práctica docente.

La neurociencia nos brinda una nueva forma de conocer al otro, nos permite ofrecerle al estudiante desafíos apropiados a la hora de enseñar y de aprender. Por lo tanto, sabemos que el niño no llega al mundo como una “tabla rasa”, posee cierta información que debemos continuar incrementando y organizando con el fin de crear conocimiento significativo.

La educación formal aspira a que los estudiantes desarrollen «un pensamiento matemático para poder interpretar críticamente la realidad, actuar sobre ella y modificarla [...] que los alumnos conjeturen, construyan argumentos, modelicen, analicen la pertinencia de los resultados obtenidos y logren comunicar los procesos y razonamientos realizados» (ANEP. CEP, 2009:67). Se pone al alumno en el centro de su propio conocimiento, guiado primero por el entorno familiar; y luego será la educación formal la que complemente y complejice el desarrollo del conocimiento matemático. Sería importante que la neurociencia y la educación trabajaran en conjunto.

Será necesario que los docentes tengamos bien claro el abordaje de los diferentes contenidos a través de prácticas didácticas adecuadas pero también de un conocimiento más profundo del funcionamiento del cerebro, para anticipar o detectar posibles inconvenientes en este desarrollo con el fin de estimular al máximo las capacidades. Volver a realizar varias veces la misma operación (por ejemplo, retrocede tres hasta llegar al número xx) sin mediar un proceso que analice esta actividad –cuáles son los patrones que se generan, por qué se llega a un número y no a otro, qué pasa con el cero en los diferentes valores posicionales– no tiene valor en el aprendizaje, no se puede volver a usar para otras situaciones. Para ello es importante que las actividades estén interconectadas, sean debidamente planificadas promoviendo espacios privados y de discusión con pares, con una oportuna intervención docente.

Sabemos que la neurociencia aporta valiosa evidencia de las respuestas neuronales a situaciones matemáticas simples o complejas, lo cual habilita a repensar las prácticas. Tenemos la oportunidad de cambiar el modelo memorístico o algorítmico de enseñanza de los conceptos matemáticos por prácticas creativas, de investigación, de construcción de conocimiento de forma autónoma y también colectiva, prácticas con fuerte sustento teórico, tal como se expuso en este artículo. Tomemos entonces la iniciativa de empezar a cambiar nuestras propuestas.

«Llegar a ser matemáticamente competente está vinculado al desarrollo de la comprensión del contenido matemático. Cuando se comprenden las nociones y procedimientos matemáticos se pueden utilizar de manera flexible, adaptándolos a situaciones nuevas y permitiendo establecer relaciones entre ellos y ser utilizados para aprender nuevos contenidos matemáticos.» (Llinares, 2006:5)