Gabriel Requena
Profesor de matemática (ANEP, 2000). Especialista en la enseñanza de la matemática (UNIPE, 2019). Formador de matemática en escuelas públicas.
La noción de proporcionalidad está presente tanto en los programas anteriores como en los vigentes de la educación primaria y de la educación media básica; sin embargo, su aprendizaje no resulta evidente. En general, los alumnos1 uruguayos de los últimos años de la escuela primaria y los alumnos de la educación media básica –y a veces del nivel superior– muestran dificultades al resolver situaciones vinculadas a la proporcionalidad (cf. INEEd, 2018; 2020). Este fenómeno, que no es exclusivo de nuestro país y tiene presencia previa a la pandemia, también se encuentra actualmente en otros sistemas educativos.
En consecuencia, parece esencial hacer que la proporcionalidad sea un contenido de enseñanza a largo plazo. Esto requiere establecer y desarrollar relaciones entre la enseñanza de los últimos años de la escuela primaria y la del comienzo de la educación media básica.
En este artículo se expone, por un lado, dónde se ubica la noción de proporcionalidad como contenido de enseñanza explícito en la Educación Básica Integrada (en adelante EBI), Plan 2023. Por otro lado, se propone una secuencia de enseñanza de la proporcionalidad para la finalización de la escuela primaria y algunas ideas para lograr su avance en el nivel medio. Al mismo tiempo, y fundamentalmente, se pretende aportar criterios y estrategias para la elaboración de secuencias de enseñanza que acompañen las trayectorias escolares.
- 1Este artículo se realiza desde una perspectiva de igualdad de género. Con el fin de agilizar la lectura se hará uso genérico del masculino, salvo que la mención explícita sea de relevancia en el contexto.
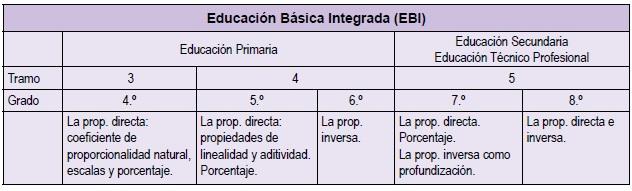
La noción de proporcionalidad en la EBI atraviesa los grados 4.º, 5.º y 6.º del segundo ciclo de
la educación primaria (ANEP, 2023a) y continúa en los grados 7.º y 8.º del tercer ciclo que abarca la educación secundaria y la educación técnico profesional (ANEP, 2023b). El plan propone un recorrido por la proporcionalidad directa, que se inicia en los grados 4.º y 5.º para retomarlo en los grados 7.º y 8.º; y por la proporcionalidad inversa a partir del grado 6.º y hasta el 8.º.
La proporcionalidad, directa e inversa, figura explícitamente en el contenido estructurante denominado “Matemática: Relaciones y funciones” en los programas vigentes (ANEP, 2023a:25; 2023b:27) en el eje “Número” desde los grados 4.º hasta 7.º, y en 8.º aparece en el eje “Variable”. En el grado 7.º, la proporcionalidad inversa figura como contenido para la profundización. Esta información se sintetiza en la siguiente tabla de elaboración propia.
Si bien no es propósito de este documento profundizar en un análisis curricular, cabe señalar
que se ofrecen nombres de nociones para orientar la enseñanza, pero resultarían insuficientes
para establecer alguna gradación del aprendizaje de la proporcionalidad. Por ejemplo, con relación a la numeración, en ninguno de los tramos se mencionan los decimales o las fracciones como otras formas de representación de la proporcionalidad.
Además no se ofrecen pistas respecto a las prácticas matemáticas que se quieren desplegar
ni al tratamiento de determinadas situaciones para preparar la introducción de la noción de
función en el Tramo 5, asunto transversal a toda la educación media básica y superior.
Tal como se indica en el título que encabeza el artículo, este texto aborda el estudio de la proporcionalidad. Al efecto, a continuación se despliega una propuesta de enseñanza para la finalización de la escuela primaria, que incluye tareas para reconocer los conocimientos de los
alumnos, problemas para enseñar la noción de proporcionalidad y las prácticas propias del hacer matemática, y actividades para sistematizar conclusiones parciales en torno a estrategias
y propiedades de la proporcionalidad.
En esta secuencia se introducen diferentes variables didácticas que inciden en la complejidad de los problemas según los tipos de tareas que enfrentan los alumnos como, por ejemplo, completar una tabla o encontrar el valor de la constante de proporcionalidad. En el mismo sentido se presentan problemas donde intervienen diferentes magnitudes y tipos de números como los naturales y los racionales.
En los primeros seis problemas se propone estudiar explícitamente la noción de proporcionalidad directa y sus propiedades en el marco de los números naturales. El problema 7 introduce los números racionales en juego con las propiedades de la proporcionalidad directa,
y desde el problema 8 se aborda la proporcionalidad inversa o cuando la relación entre cantidades no es proporcional.
→ Problema 1
a. Para el festival de la escuela, la panadería preparó una oferta de 5 alfajores por $25. Para
saber cuánto tendría que pagar la escuela según la cantidad de alfajores que compre, se hizo esta tabla. Complétala.
| Alfajores | 5 | 10 | 15 | 20 |
| $ |
b. Anota en qué te fijaste para completarla y compara tus anotaciones con tus compañeros.1
c. Además, la panadería elaboró ojitos con membrillo a un precio especial de $3 cada uno
para el festival de la escuela. Completa la siguiente tabla:
| Ojitos | 30 | 40 | 200 | |||
| $ | 3 | 30 | 150 |
|
Comentario didáctico |
→ Problema 2
En un kiosco tienen para la venta 6 cajas con la misma cantidad de alfajores. Si entre las 6 cajas hay 72 alfajores, ¿cuántos alfajores habrá en 18 cajas del mismo tipo? ¿Y en 9 cajas? 2
| Comentario didáctico A diferencia del problema anterior, el alumno podrá decidir si necesita o no ordenar los datos en una tabla. Los números involucrados permiten utilizar relaciones de “doble” y “mitad” para encontrar las cantidades solicitadas. Para averiguar cuántos alfajores habrá en 18 cajas, se podría encontrar la relación entre 18 y 6. El valor correspondiente a 9 cajas, podría obtenerse a partir de la mitad del correspondiente a 18 cajas. |
→ Problema 3
a. Camila es una nadadora de 16 años y vive en Centenario. Últimamente ha logrado muy buenos tiempos en sus entrenamientos en el estilo espalda, aunque su nuevo desafío se centra
en la cantidad de metros nadados. Completa la siguiente tabla sabiendo que Camila mantiene siempre la misma velocidad de nado.
| Tiempo en segundos | 18 | 108 | |||
| Distancia recorrida en metros | 20 | 40 | 60 | 140 |
| Comentario didáctico En este problema aparecen magnitudes de distinta naturaleza. Por un lado, el tiempo (medido en segundos) y, por el otro, la distancia recorrida (medida en metros), y se hace explícito en el enunciado que Camila nada a una velocidad constante. Tengamos en cuenta que esta aclaración es necesaria para que podamos considerar que se trata de una relación de proporcionalidad directa. Es la que garantiza que para recorridos iguales se emplean tiempos iguales. |
b. Escribe al lado de cada cálculo la información de la situación que ese cálculo te permite identificar. Te ofrecemos un ejemplo.
18 x 3 Con este cálculo averiguamos la cantidad de segundos que le lleva a Camila nadar 60 metros (que es triple de 20 metros).
20 x 7 ................................................................
18 + 36 ..............................................................
| Comentario didáctico Apoyado en el trabajo de completar la tabla en la parte a., en esta se deberán interpretar los cálculos propuestos para relacionarlos con las estrategias utilizadas donde se pondrían en juego las propiedades de la proporcionalidad. |
c. En crol, otro de los estilos que nada Camila, registró los siguientes tiempos según los metros que nadó.
| Tiempo en segundos | 18 | 34 | 50 | 110 | 139 |
| Distancia recorrida en metros | 20 | 40 | 60 | 120 | 140 |
Comparen el registro presentado en la parte a. con este. ¿Qué diferencias encuentran? ¿Por qué se pudieron haber dado?
| Comentario didáctico En esta parte se espera que al comparar los registros indicados se identifique que la velocidad de nado no es constante. Asimismo, que los alumnos estudien las variaciones en su velocidad en ciertos intervalos. Se podría interpretar el significado de una de las constantes de proporcionalidad como la velocidad. |
→ Problema 4
a. Sabiendo que estas son tablas de proporcionalidad directa, complétalas.
| 40 | 20 | 60 | 100 | 140 | 200 |
| 560 |
| 5 | 6 | 7 | 9 | 11 | 21 |
| 35 |
| 4 | 5 | 6 | 7 | 9 |
| 68 | 85 |
b. Comparte las tablas con tus compañeros.
¿A todos les sirvió la misma estrategia para completarlas?3
| Comentario didáctico Los alumnos podrían completar las tablas sin explicitar las propiedades de la proporcionalidad que utilizaron. Con la parte b. se pretende que en la interacción con sus pares puedan identificarlas, indicarlas, nombrarlas y observar que puede haber propiedades diferentes a las puestas en juego por cada uno de ellos. En estos casos no se informa el valor de la constante de proporcionalidad o valor unitario, como es usual en los problemas presentados en el primer ciclo o en la parte c. del Problema 1 de esta secuencia. Este asunto es importante porque incide en la complejidad del problema y sobre la variedad de procedimientos que pueden desplegarse. El trabajo con tablas por parte de los alumnos tiene enormes ventajas, pero señalemos dos advertencias sobre su uso. Para mitigar la ocurrencia de ciertos errores, Block, Mendoza y Ramírez (2015) sugieren evitar poner siempre los valores siguiendo alguna regularidad (por ejemplo, 5, 10, 15, 20) o sin regularidad alguna (por ejemplo, 5, 15, 45, 100). Por otro lado, si es la única forma de presentar los datos o su frecuencia de uso en el aula es alta, los alumnos podrían asociar directamente esta forma de organización (tabla) con las propiedades puestas en juego. Por ello es además necesario proponer problemas que permitan reflexionar sobre la idea de que no todas las relaciones involucradas en una tabla son de proporcionalidad directa. Una de las situaciones que se proponen a continuación puede abonar a esta reflexión. |
→ Problema 5
Identifica cuáles situaciones siguientes son de proporcionalidad directa y explica por qué.
a)
| Área a pintar en metros cuadrados | 1 | 4 | 9 | 12 | 20 |
| Precio en pesos para pintar | 450 | 1800 | 4050 | 5400 | 9000 |
b) Si para recorrer 350 km mi auto consume 40 litros de nafta. ¿Cuánto combustible consumirá
para recorrer 700 km?
c) Cuando Irene cumplió 5 años, su mamá tenía 37 años. ¿Cuántos años tendrá la mamá
cuando Irene cumpla el triple de sus años?
d)
| Cantidad de cajas | 2 | 4 | 6 | 10 | 20 |
| Cantidad de comprimidos | 14 | 28 | 44 | 700 | 980 |
e) En el supermercado, un litro de leche chocolatada cuesta $73. ¿Cuánto cuestan 3 litros si
no se hace descuento por cantidad?
| Comentario didáctico Esta “actividad de cierre” del trabajo de relaciones entre cantidades pretende evidenciar dificultades de la enseñanza y del aprendizaje de la proporcionalidad directa en el marco de los números naturales, y la necesidad o no de realizar nuevas aproximaciones a este concepto. «...elaboramos una primera caracterización de la actividad de cierre como aquella que genera condiciones para revisitar, para rever las tareas o los conocimientos más importantes desplegados en los problemas ya trabajados en clase. Esta actividad, de tipo resumen más que de “frecuentación”, apuntaría a reorganizar los conocimientos de los alumnos y a tomar nuevos apuntes sobre lo ya trabajado.» (Correa, Pérez y Requena, 2020:132) En esta actividad resultará importante identificar que hay relaciones en las que, al aumentar o disminuir una de las cantidades, aumenta o disminuye la otra, y no son de proporcionalidad. Esta es una generalización habitual que debiera problematizarse para evitar futuros errores. Luego de este momento de cierre, el docente podría registrar el estado de conocimiento de los alumnos identificando los avances en sus conocimientos, por ejemplo, en el portafolio docente que compile las producciones de cada uno de ellos. |
→ Problema 6
La mamá de Julia decidió comprarle un celular por primera vez a su hija optando por un plan para niños. En las vacaciones, Julia habló 210 minutos en el mes de enero y la mamá quiere
saber cuánto va a tener que pagar, pero no recuerda cuál es el precio por minuto hablado. Por ello, decide anotar en una tabla el tiempo aproximado que Julia habló y lo que pagó en los primeros cinco meses, ordenados de menor a mayor según el tiempo que habló.
| Tiempo de llamadas en minutos | 94 | 105 | 116 | 140 | 167 |
| Monto pagado en pesos | 291,40 | 325,50 | 359,60 | 434 | 517,70 |
Analicen las siguientes estrategias para afirmar si les permiten o no calcular lo que la mamá de Julia deberá pagar por 210 minutos.
a. Cuando habló 94 minutos se pagó $291,40 y por 116 minutos se pagó $359,60. Entonces
por 210 minutos se pagará $291,40 + $359,60 = $651.
b. Al observar los tres primeros valores se ve que cada 11 minutos se paga $34,1 más. Entonces $34,1 dividido 11, es $3,1 que es lo que cuesta el minuto. Para saber cuánto debe pagar por 210 minutos hace $3,1 x 210.
c. Cuando habló 140 minutos se pagó $434, entonces por 14 minutos se pagará $434:10 =
$43,4 y por 70 minutos se pagará: $43,4x5 = $217. Entonces, sumando lo pagado por 140
minutos más lo de 70 minutos, se obtiene lo que se pagará por 210 minutos.
| Comentario didáctico En este caso se presenta una “actividad de reinversión”, pues los conocimientos trabajados se involucran en las estrategias ofrecidas pero hay un nuevo asunto: los alumnos deben analizar un razonamiento hecho por otro, es decir, no propio, para decidir cuánto hay que pagar y también poner en juego números racionales expresados como decimales. No para todos los alumnos resulta sencillo suponer que se sostienen las propiedades de la proporcionalidad directa con la aparición de las expresiones decimales. Según considere el docente, se podría habilitar el uso de la calculadora para evitar que los cálculos sean un posible obstáculo y para que los alumnos se centren especialmente en las relaciones entre las cantidades. En este punto de la secuencia, algunos alumnos podrían considerar cuál estrategia convertir en la suya, en propia, y argumentar en qué se basa esa decisión. |
→ Problema 7
Los socios de un club alquilarán un ómnibus para salir de excursión. Se anotaron 20 personas
para ir. El ómnibus cobra $8000 y tiene capacidad máxima de 42 personas.
a. ¿Cuánto tendrá que pagar por el transporte cada socio que se anotó?
b. ¿Cuánto pagará cada uno si van 25 socios?
c. Bárbara dice que quisiera que se anotaran otros 20, así cada uno pagaría la mitad. ¿Es correcto lo que dice? Explica tu respuesta.
d. ¿Cuántos socios deberían viajar para que cada uno pague menos de $220?
e. ¿Cuál es el precio mínimo que podrían pagar los socios por el transporte?
f. Completa la siguiente tabla.
| Cantidad de socios que viajan | 20 | 24 | 32 | 36 | 38 | 40 | 41 | 42 |
| Precio que paga cada uno ($) |
g. ¿El precio que paga cada socio es directamente proporcional a la cantidad de socios que van de excursión? Si te parece que sí, encuentra la constante.4
| Comentario didáctico En este problema, a diferencia de los anteriores, las dos cantidades no varían de la misma manera: cuando una aumenta, la otra disminuye (en la misma proporción) y viceversa. Resultará importante generar condiciones para que los alumnos puedan poner en palabras sus ideas y elaboren explicaciones. En este sentido, hay que tener presente que es complejo entender qué es una explicación matemáticamente pertinente y qué no, pues no existe una norma clara con la cual contrastar para “controlar” las explicaciones (cf. Sadovsky, 2010). |
→ Problema 8
Escribe posibles dimensiones para los lados de un rectángulo de 18 cm2 de área.
| Comentario didáctico Este problema enfrenta a los alumnos a proponer posibles dimensiones de medida de lados y a decidir nuevamente si necesitan o no ordenarlas en una tabla. Es deseable que las medidas de los lados que propongan los alumnos incluyan números racionales que estén entre 1 y 18. En caso de no ser así, el docente decidirá la conveniencia o no de hacerlo él. Organizar los valores en una tabla favorecería el análisis de la propiedad característica de la proporcionalidad inversa (si una cantidad se duplica, la correspondiente se reduce a la mitad, si una cantidad se triplica, la correspondiente se reduce a la tercera parte...). |
→ Problema 9. Tarea de estudio
a. Ejemplifica el uso de las propiedades de las relaciones de proporcionalidad directa que se expresan a continuación.
► Dos magnitudes son directamente proporcionales cuando al doble, al triple, a la mitad, al tercio, etc. de la cantidad de una magnitud le corresponde el doble, el triple, la mitad, el tercio, etc. de la cantidad correspondiente de la otra magnitud.
► Dos magnitudes son directamente proporcionales cuando a la suma o resta de las cantidades de una magnitud, le corresponde la suma o resta de las cantidades correspondientes de la otra magnitud.
► Dos magnitudes son directamente proporcionales cuando al realizar el cociente entre cada par de cantidades que se corresponden, se obtiene el mismo número. Este número se llama constante de proporcionalidad.
b. Busquen en las diferentes situaciones abordadas alguna relación entre cantidades que no sea de proporcionalidad y explicar por qué no lo es.
| Comentario didáctico Esta tarea propone retomar el trabajo con los enunciados y las resoluciones de las actividades anteriores. En ese sentido, se plantea un retorno reflexivo sobre lo que se ha hecho para relacionarlo con los conocimientos y reconocer avances por parte de los alumnos. Esencialmente tiene el propósito de volver a las propiedades vistas para pensar situaciones donde ellas se pongan en juego. «De esta manera, se está enseñando a los alumnos a organizar un repaso, que no necesariamente debe realizarse antes de una prueba, sino que puede hacerse en cualquier momento del aprendizaje e irse completando.» (Napp et al., 2005:18) |
Como ya se mencionó, la secuencia didáctica aquí propuesta se centra en el trabajo con la noción de proporcionalidad y con prácticas propias del hacer matemático. En este apartado se tratará de ofrecer algunas ideas para pensar en la enseñanza de la proporcionalidad para el
nivel medio, recuperando el trabajo realizado en la educación primaria.
La noción de proporcionalidad directa abarca una variedad de conceptos y de relaciones que deben continuar entramándose. En el nivel medio está muy asociada en general a la resolución de problemas, por ejemplo, de cálculo de porcentajes donde la única estrategia de resolución es la regla de tres simple. En relación con ello, se sugiere realizar un trabajo a partir del estudio de las propiedades de la proporcionalidad para que sirvan de puntos de apoyo genuino al momento de argumentar por qué funciona dicha regla. Este trabajo contribuiría a un uso más reflexivo de la regla de tres y a que los alumnos puedan controlar si el resultado obtenido tiene o no sentido en el contexto del problema resuelto.
Asimismo, el trabajo con la proporcionalidad y sus propiedades que se propuso en la secuencia contribuiría para que los alumnos continúen elaborando la idea de variable.
«Concebir este tipo de relación como procesos de cambio habilitaría la posibilidad de iniciar a los alumnos en un trabajo que asuma características algebraicas y requiera el uso de otros modos de representación, como las fórmulas o los gráficos. El estudio de las propiedades vuelve desde otra perspectiva contribuyendo a una profundización del concepto.» (Broitman et al., 2018:10)
En ese sentido, recuperar el trabajo con las propiedades resultará potente para avanzar en el estudio de la proporcionalidad como función. Se sugiere hacer un trabajo explícito y sistemático en torno a situaciones en las que una magnitud depende de otra, de manera que para aumentos iguales en una de ellas corresponderán aumentos iguales en la otra.
Proponer problemas con variaciones resulta fundamental para introducir el conocimiento sobre el objeto función, para la producción de otros registros de representación (fórmulas y gráficos) y la coordinación entre ellos, y para construir sentido respecto de la función lineal diferenciándola de la función de proporcionalidad.
En términos de tareas, convendría continuar ampliando estrategias de estudio que enriquezcan
el proceso de todos los alumnos como, por ejemplo, pedir que elaboren machetes1
para luego
reelaborarlos colectivamente en el aula.
- 16 Para conocer sobre la idea y su implementación se sugiere la lectura de Napp et al. (2005).
En este artículo se plasmó una secuencia de enseñanza para la finalización de la escuela primaria en torno a la noción de proporcionalidad y se presentaron algunas ideas para la continuidad de su enseñanza en el nivel medio, apoyadas en las nociones y prácticas matemáticas desplegadas en la secuencia.
Asimismo, se puso de relieve un conjunto de tareas (de diagnóstico, de reinversión, de cierre, de estudio, de sistematización de los conocimientos y de las estrategias utilizadas), y criterios de articulación de nociones y prácticas matemáticas que permitan a los docentes apoyar sus decisiones para la elaboración de secuencias de enseñanza que acompañen las trayectorias de los alumnos.