A continuación se muestran las actividades  que fueron seleccionadas para abordar en este artículo. Su elección está relacionada con la intencionalidad de mostrar cómo elaborar posibles secuencias que cubran un amplio rango de dificultad, a partir de tareas pertenecientes a distintos contenidos programáticos.

El análisis de las actividades se centra en algunos de los procesos cognitivos que se ponen en juego en la resolución de la tarea, y se plantean ideas que permitirían adaptar la actividad a distintas formas de hacer Matemática. En este sentido, al modificar la complejidad de las actividades, el docente puede tomar insumos para contemplar secuencias para distintos grados escolares. Asimismo, se puede encontrar un correlato de los procesos cognitivos puestos en juego en cada actividad elegida, así como en cada modificación propuesta, en los niveles de desempeño del INEEd (INEEd, 2019).

Las actividades elegidas son de múltiple opción y se presentan junto al porcentaje de alumnos que respondió correctamente a cada una de ellas en la evaluación nacional Aristas 2017 (INEEd, 2018), lo que permite obtener información acerca de su dificultad1. En el momento de optar por usar estas actividades para llevar al aula o para conformar una secuencia no es necesario que también se aplique el modelo de múltiple opción, sino que el maestro puede presentar la actividad en distintos formatos. En las sugerencias presentadas se consideran algunas  alternativas.

Esta actividad presenta una serie de números naturales, que aumenta en forma aditiva de modo constante. La consigna es encontrar la relación entre cada número y su siguiente; es decir, identificar la regularidad de la serie, expresada en lenguaje natural.

En la Aristas 2017, esta actividad fue resuelta correctamente por el 45,5%. Al contar con cuatro opciones de respuesta, los alumnos podrían elegir la primera opción, que es una de las que permite pasar del primer al segundo término de la serie. Sin embargo, quienes responden correctamente logran “saltear” este obstáculo, para identificar que la regularidad presente entre todos los pares consecutivos de números es +4.

Una posible adaptación de la actividad manteniendo la consigna, consistiría en hacer la pregunta “abierta”. Es decir, no dar opciones de respuesta, sino habilitar a que sean los alumnos quienes encuentren la relación entre un número y el siguiente en la serie. Ese tipo de actividad permite, por un lado, que sean los alumnos “sin ayuda” quienes tengan la responsabilidad de identificar la regularidad presente. A su vez, el ejercicio de escribir dicha regularidad consistiría en una tarea que se centra en la habilidad de escritura y comunicación en Matemática.

Por otra parte, también se podría adaptar esta actividad conservando la regularidad numérica, pero modificando la pregunta. Por ejemplo, si se pidiera completar la serie con el término siguiente, los alum- nos tendrían que identificar el “+4” involucrado y aplicarlo al 14. Este tipo de tarea estaría más centrado en identificar la regularidad y aplicarla, pero no involucraría la escritura de dicha regularidad.

En la misma línea de completar la serie, se les podría dar a los alumnos una serie en la que falte algún término intermedio, o el primero, para que la completen:

Los procesos cognitivos puestos en juego para resolver esta actividad son más complejos que los requeridos para completar con el término siguiente, ya que no es tan sencillo identificar la regularidad y, a su vez, la actividad implicaría “ir para atrás” con los términos.

Otro tipo de modificación podría ser pedirles a los alumnos que identifiquen si un cierto número pertenece a la serie. Por ejemplo: “Si seguimos escribiendo esta serie de números, ¿estará el 44?”.

Por otra parte, una variación didáctica que afectaría la dificultad es alterar el rango numérico de la serie usando números más grandes, o cambiando la regularidad para que involucre una cantidad constante más “difícil”.

Ahora bien, el trabajo con regularidades numéricas se continúa durante la escolaridad y puede cambiar en su complejidad. En este escenario también es posible considerar secuencias didácticas, en las que se pasa de un término al siguiente haciendo una sustracción o una multiplicación. La elección del tipo de regularidad y la constante aditiva o multiplicativa también abre un abanico de posibilidades de variables didácticas, a tener en cuenta a la hora de diseñar una secuencia.

1 Para obtener mayor información acerca de los porcentajes de respuesta de cada opción, consultar INEEd (2019).

En esta actividad, los alumnos tienen que interpretar la situación y reconocer la operación que la modeliza. La opción correcta fue elegida por el 41,1% de los alumnos, mientras que casi un 25% optó por la opción A (una sustracción entre los montos correspondientes a cada clase).

La resolución de la actividad implica leer cuidadosamente la información presentada, ya que si no se interpreta el sentido de la adición del modo en que está contextualizada, se puede asumir que el problema consiste en identificar cuánto falta recaudar, y no cuánto se debe recaudar en total. En efecto, eso es lo que probablemente hayan pensado los alumnos que eligieron la opción A. 

El abordaje de los distintos significados de las operaciones es un aspecto muy relevante, y poner el foco en la modelización de operaciones y no so- lamente en la aplicación de algoritmos de cálculo aporta a su conceptualización (Rodríguez Rava y Silva Palumbo, 2002). En este caso, que involucra una adición, la situación está dada y los alumnos de- ben elegir la operación que permite resolverla. Una primera variable didáctica a modificar podría ser pre- sentar la pregunta sin opciones de respuesta para recoger todos los posibles errores de los alumnos, lo que también habilita al maestro a trabajar a partir de ellos. Asimismo, una tarea que también habilita el trabajo de modelización consiste en darles a los alumnos el planteo de una operación, y pedirles que ellos propongan situaciones que tenga sentido re- presentar a través de la operación planteada. Este tipo de tarea se puede realizar para las cuatro operaciones básicas, y favorece la concientización de los distintos sentidos de las operaciones. Por ejemplo, se podría plantear:

Estas tareas permiten mostrar la conceptualización que tienen los alumnos sobre la operación y el significado que le otorgan no solo a la operación en sí, sino también al sentido y pertinencia del contexto elegido. A partir de las producciones de los alumnos, en clase se puede habilitar una discusión sobre la pertinencia de las situaciones propuestas. Por ejemplo, la situación...

...no es de un contexto real más allá de que efectivamente pueda resolverse con la operación plantea- da, debido a que en los ómnibus no pueden viajar ciento quince personas. Los distintos significados de las operaciones se deberían relacionar también con su aplicación en contextos auténticos, para su mejor conceptualización. Más aún, el trabajo de modelización a través de operaciones favorece la resolución exitosa de situaciones enmarcadas en contextos donde los alumnos no sean guiados para utilizar cierta operación en particular.

Cabe destacar que el ejercicio de “traducir” una situación del lenguaje natural al registro aritmético, y recíprocamente, más allá de la operación matemática que implique, involucra un dominio de ciertos códigos de la lectura y de la escritura en Matemática. Estas habilidades deben ser enseñadas para que los alumnos ganen autonomía en su quehacer matemático (Rodríguez Rava y Arámburu Reck, 2016). 

En esta actividad se presentan cuatro instrumentos de medida, y los alumnos deben elegir cuál de ellos se usa para conocer el peso de un niño. Si bien es una tarea que no parece tener mayor complejidad, solo el 70,8% de los alumnos la respondió correctamente. La identificación de los instrumentos de medida con las magnitudes que estos permiten medir, constituye un primer paso para el uso efectivo de estos instrumentos para la medición y la conceptualización de las magnitudes (Chamorro, 1995).

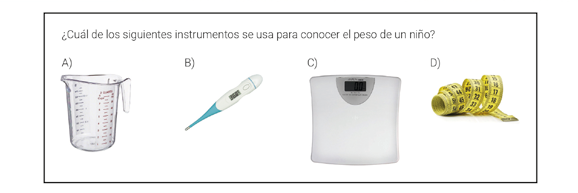
Un posible matiz de la actividad para obtener una tarea más sencilla podría consistir en preguntar acerca de un instrumento de longitud, ya que estos son los más cercanos a los alumnos en tercer grado. Por otra parte, una posible modificación para trans- formar la pregunta en “abierta” sería consultarles a los alumnos acerca del nombre del instrumento que se usa para conocer el peso de un niño.

Para avanzar en una secuencia didáctica, se les podría pedir a los alumnos que estimen longitudes  a partir de varios referentes dados. La realización  de prácticas efectivas de medición habilita la conceptualización de la medida de magnitudes. En un primer momento, se les puede proporcionar a los alumnos una unidad de medida de longitud como un “palito” y plantearles que midan longitudes a partir de la del palito. Del mismo modo, se pueden utilizar otros referentes para realizar prácticas de medición de otras magnitudes. Este tipo de prácticas abona  a la comprensión de las medidas de magnitudes en cuanto refleja ciertas dificultades inherentes al proceso de medición (Chamorro, 2003): la existencia de cierto grado de error en las mediciones, la necesidad de estimar, la posibilidad de considerar distintos referentes como unidad de medida y, por lo tanto, distintas unidades, la existencia de unidades de medida convencionales y no convencionales, y otras.

Volviendo a la actividad planteada, resulta relevante que un 11,6% de los alumnos eligió la opción D como correcta. Quizás, si en lugar de una cinta métrica hubiera habido una regla, el porcentaje habría sido aún mayor. Esto podría poner de manifiesto el lugar privilegiado de la longitud como unidad de medida utilizada en la escuela. Para abordar este obstáculo, se pueden proponer actividades referidas a objetos que soporten distintas magnitudes a considerar, y plantear preguntas que permitan discutir dicha situación. Por ejemplo:

Estas preguntas pueden habilitar la discusión en clase sobre la superficie de la mesa, así como sobre sus dimensiones. El maestro puede preguntar si es necesario saber el peso de la mesa de luz para la situación planteada, pero también pedirles a los alumnos que piensen una situación en la que sea necesario conocer su peso para responder la pregunta. En cursos superiores también se podría preguntar acerca de la utilidad de conocer el volumen de la mesa de luz.

En esta actividad se presenta una tabla de frecuencias acerca de una variable cualitativa. Observando  la información de la tabla, los alumnos deben identificar cuál es el deporte con mayor cantidad de votos (la moda). La actividad fue resuelta acertadamente por el 72,6% de los alumnos2 y fue una de las más sencillas de la prueba de Estadística.

La tabla presentada puede servir de soporte para varias actividades que abarquen un amplio rango de dificultad, lo que  permitiría  avanzar  en los desempeños de los alumnos. Por ejemplo, se puede usar para buscar otros datos explícitos como preguntar acerca de cuáles fueron los deportes que eligieron los alumnos o cuál fue el menos votado, o cuántos alumnos eligieron “Tenis”. También se puede usar la tabla para que los alumnos identifiquen información implícita, como cuántos alumnos votaron por deportes de pelota o que se juegan en una cancha.

Otro tipo de tarea que se puede realizar a partir de esta tabla es pedirles a los alumnos que construyan un gráfico de barras que muestre la misma información que la tabla, o bien que extraigan conclusiones que involucren información implícita en ella. Por ejemplo, “¿cuántos alumnos respondieron la encuesta?”. Estas preguntas resultan aún más complejas si la información se presenta directa- mente en un gráfico y no en la tabla ya que, antes de sumar las cantidades, los alumnos deben identificar la frecuencia de cada valor de la variable. Un ejemplo de este tipo de tareas se presenta en la siguiente actividad.

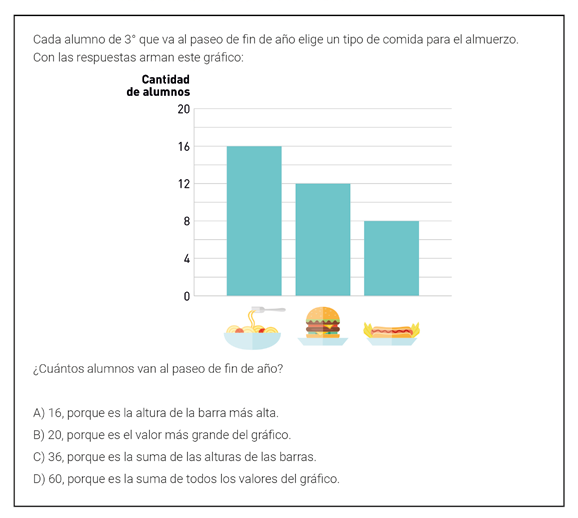
Esta actividad fue resuelta por la  cuarta parte de los alumnos lo que, tal como se comentó anteriormente, refleja una complejidad mayor. El maestro podría proponer la actividad en clase sin las opciones de respuesta y pedir una justificación, de modo que los alumnos tengan que interpretar y discutir acerca de qué información usar,   y cómo hacerlo. Eventualmente, para la  puesta  en común, podría tomar distintas alternativas que hayan surgido o no en su clase (para esto podría basarse en las alternativas de respuesta de la actividad). Así, pondría en discusión cada una de las alternativas,  abonando a la interpretación  de información provista en el gráfico. Cabe mencionar que la opción A fue elegida por más del 45% de los alumnos. Esto podría indicar que ellos bus- can información “a la vista” en el gráfico, y es un posible punto de partida para favorecer avances en clase.

Del mismo modo que se puede usar una tabla como soporte para distintas actividades de una secuencia, este gráfico también podría usarse para diseñar actividades más sencillas que respondan a preguntas como “¿cuál fue el almuerzo más elegido?” o “¿cuántos alumnos eligieron hamburguesas?”.

2 Un 17,7% de los alumnos eligió la respuesta “Fútbol”, quizás por su alta popularidad.

Esta actividad de Geometría involucra la clasificación de figuras del plano según la congruencia de sus ángulos. Fue respondida correctamente por el 21% de los alumnos, mientras que casi el 50% eligió la opción A (los polígonos que tienen sus lados congruentes).

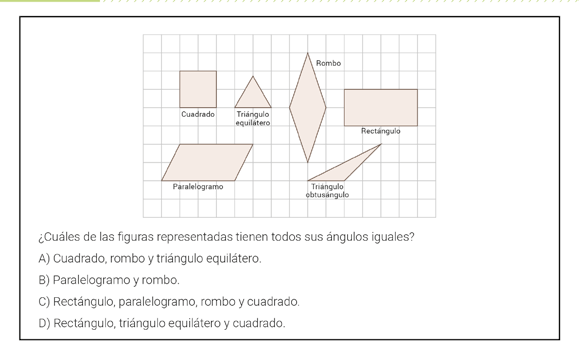
Más allá de la complejidad propia de la actividad, toda la información que se presenta (seis figuras de las cuales hay que elegir algunas, leer cuatro opciones de respuesta, los nombres de las figuras, el cuadriculado) hace que sea más difícil llegar a la respuesta correcta. Sin embargo, es posible usarla como disparador para trabajar distintas formas de clasificar figuras planas. Por ejemplo: 

Si se piensa en actividades de Geometría que habiliten procesos cognitivos más sencillos, se podrían borrar los nombres de las figuras y pedirles a los alumnos que identifiquen el cuadrado, el rombo, etcétera. La cuadrícula permite que los alumnos pue- dan asegurar que ciertos ángulos son o no rectos, o que algunas longitudes sean o no congruentes. Sin embargo, este tipo de interpretación de códigos matemáticos no es natural, y debe ser enseñado para que los alumnos puedan trabajar con autonomía usando esta información.

Por otra parte, esta actividad se podría usar también de soporte para que los alumnos construyan legajos de las figuras presentadas. Un juego para trabajar esta habilidad de descripción, involucrando la lectura y la escritura en Matemática, sería:

Las actividades de escritura de legajos habilitan que los alumnos identifiquen las características de un objeto matemático que consideran relevantes. A su vez, favorecen la escritura de ideas que muchas veces se expresan oralmente en la clase, pero no  se hace el ejercicio de escribirlas. Por otra parte, el hecho de que un compañero tenga que leer la tarjeta permite trabajar cuestiones relacionadas con la lectura en Matemática y, en particular, la interpretación de información que describe objetos matemáticos. Seguramente, algunas descripciones hagan referencia a la cantidad de cuadraditos de las figuras. Eventualmente, para propiciar avances en las descripciones de figuras, el maestro debería proponer actividades que no tengan cuadrícula, o bien que incluyan otro tipo de información, para que los alum- nos puedan prescindir de las medidas específicas de los lados de las figuras. A fin de favorecer la discusión en clase acerca de las descripciones, el maestro puede tener algunas tarjetas ya “prontas” para leer en voz alta y los alumnos tengan que identificar de qué figura se trata. Por ejemplo:

Otro tipo de tarea similar, pero sin utilizar las figuras dadas, podría ser que el maestro describa figuras para que los alumnos dibujen, y luego todos deben mostrar sus dibujos para ver si coinciden o no. El maestro podría elegir la información de las descripciones para que en los primeros casos la figura descrita sea única, pero eventualmente se habiliten distintas opciones. Así, la actividad consistiría en un punto de partida para trabajar sobre características y propiedades de las figuras.

Las actividades propuestas son algunas de las presentadas en Aristas en clase de tercero de primaria para evaluar Matemática. El objetivo del artículo es analizar posibles usos y abordajes de la información que brinda la evaluación estandarizada. En este caso, se hizo a partir de la evaluación nacional. Sin embargo, propuestas similares se pueden realizar tomando actividades liberadas de otras evaluaciones estandarizadas. Además, tal como se mencionó anteriormente, las secuencias se pueden diseñar para aplicar en otros cursos, y no exclusivamente en tercero de primaria.

El estudio de posibles procesos cognitivos y procedimientos de los alumnos busca orientar al maestro en la organización de secuencias didácticas que abarquen distintos aspectos de la competencia matemática. Asimismo, se pueden tener en cuenta los niveles de desempeño del INEEd, que reflejan actividades que involucran los procesos cognitivos y los distribuyen en términos de la dificultad que estas requieren, para que las secuencias abarquen también los distintos niveles de dificultad.

La evaluación estandarizada de bajas consecuencias (como Aristas, TERCE o PISA) tiene como objetivo brindar información acerca del estado de los desempeños de los estudiantes. A partir de la información que estas evaluaciones presentan, como actividades liberadas y sus porcentajes de respuestas, niveles de desempeño de los alumnos, etc., los docentes pueden orientar la organización de sus cursos, poniendo el foco en los aspectos didácticos que consideren que los alumnos requieran trabajar. Asimismo, los datos proporcionados por la evaluación externa pueden servir de insumo para la discusión y reflexión del colectivo docente, y para la posible interpretación de desempeños en el grupo o en la escuela.

CHAMORRO, María del Carmen (1995): “Aproximación a la medida de magnitudes en la Enseñanza Primaria” en Uno. Revista de Didáctica de las Matemáticas, Nº 3. Barcelona: Editorial Graó.

CHAMORRO, María del Carmen (2003): “Las dificultades en la enseñanza-aprendizaje de las magnitudes en Educación Primaria y Secundaria” en Separata de QUEHACER EDUCATIVO, Nº 58 (Abril). Montevideo: FUM-TEP.

INEEd (2018): Aristas 2017. Informe de resultados de tercero y sexto de educación primaria. Montevideo: INEEd. En línea: https://aristas2017.ineed.edu. uy/InformeAristas2017.pdf

INEEd (2019): Aristas en Clase: matemática en tercero de primaria. Documento de apoyo al docente. Montevideo: INEEd. En línea: https://www.ineed. edu.uy/images/Aristas/AristasEnClase/DocumentoDeApoyo/AristasEnClase-2017-Primaria-Matematica-3.pdf

RODRÍGUEZ RAVA, Beatriz; ARÁMBURU RECK, Graciela (coords.) (2016): El hacer Matemática en el aula. Un puente hacia la autonomía. Colección matemática, 1. Montevideo: FUM-TEP/Fondo Editorial QUEDUCA.

RODRÍGUEZ RAVA, Beatriz; SILVA PALUMBO, Alicia (2002): “La apropiación de las Operaciones Matemáticas. Algunas teorizaciones acerca de los Contextos y los Significados en el marco de la enseñanza escolar” en QUEHACER EDUCATIVO, Nº 51 (Febrero), pp. 49-52. Montevideo: FUM-TEP.